How to figure odds

Odds of 7/2 will pay times the bet amount, so for example, a $ bet placed on 7/2 fractional odds will return $ in profit. A $ bet placed on 2/7. So the odds are p: q = = 28 = 7 in favor. Example 4. Find the appropriate odds if. (i) P(A) = 5. 7. (ii). Example 3. Calculate the odds in favor of spinning a how to figure odds. First, find the favorable and unfavorable outcomes. Next, write the ratio of. The formulas for odds in favor and odds against are shown below in two different ways. One way shows how to find odds if you know the number of.

Odds Calculator

How do you calculate payout with odds? In order to calculate your potential payout you simply multiply your stakes (the amount of money you wagered) by the odds. For example, if you bet $100 on the Pistons beating the Knicks at 2.25 odds, your total potential payout would be $225 ($100 x 2.25).

What is the odds ratio formula? In a 2-by-2 table with cells a, b, c, and d (see figure), the odds ratio is odds of the event in the exposure group (a/b) divided by the odds of the event in the control or non-exposure group (c/d). Thus the odds ratio is (a/b) / (c/d) which simplifies to ad/bc.

How do you calculate chance? You calculate probability by dividing the number of successes by the total number of attempts. Your result will be a number between 0 and 1, which can also be expressed as a percent if you multiply the number by 100%.

What does minus 150 odds mean? The number that follows the negative symbol (the odds) reveals how much to bet for every $100 you want to win. For example, if the team you're betting on has -110 odds, you need to wager $110 to win $100. If your team has -150 odds, you must risk $150 to win $100.

What does an odds ratio of 0.25 mean? The OR of 0.25 means that the odds of developing influence are 25% as high (or 75% lower) for the treatment group compared to the placebo group.

How do you calculate odds? Calculating Odds from Probability

What is an odds ratio example? For example, an odds ratio for men of 2.0 could correspond to the situation in which the prob- ability for some event is 1% for men and 0.5% for women. An odds ratio of 2.0 also could correspond to a probability of an event occurring 50% for men and 33% for women, or to a probability of 80% for men and 67% for women.

What is the formula for simple probability? P(A) = n(A)/n(S)

Odds Probability Calculator

Consequently, the odds ratio provides a relative measure of effect for case-control studies, and it provides an estimate of the risk ratio in the source population, provided that the outcome of interest is uncommon. We emphasized that in case-control studies the only measure of association that can be calculated is the odds ratio.

However, in cohort-type studies, which are defined by following exposure groups to compare the incidence of an outcome, one can calculate both a risk ratio and an odds ratio. As with a risk ratio, the convention is to place the odds in the unexposed group in the denominator. In addition, like a risk ratio, odds ratios do not follow a normal distribution, so we use the lo g transformation to promote normality.

As a result, the procedure for computing a confidence interval for an odds ratio is a two step procedure in which we first generate a confidence interval for Ln OR and then take the antilog of the upper and lower limits of the confidence interval for Ln OR to determine the upper and lower limits of the confidence interval for the OR.

The two steps are detailed below. The null, or no difference, value of the confidence interval for the odds ratio is one. We again reconsider the previous examples and produce estimates of odds ratios and compare these to our estimates of risk differences and relative risks. This gives the following interval 0. Interpretation: The odds of breast cancer in women with high DDT exposure are 6.

The null value is 1, and because this confidence interval does not include 1, the result indicates a statistically significant difference in the odds of breast cancer women with versus low DDT exposure. Therefore, odds ratios are generally interpreted as if they were risk ratios. Note also that, while this result is considered statistically significant, the confidence interval is very broad, because the sample size is small.

As a result, the point estimate is imprecise. Notice also that the confidence interval is asymmetric, i. A 1 in chance of winning, or probability of winning, may be reported as "1 in " or "1 out of These all most likely mean 1 chance of winning out of total possible outcomes. Therefore, in terms of odds, this means "1 to odds for winning" which is exactly the same as " to 1 odds for losing.

For example, a Pick 3 lottery has a total of possible outcomes, from to So a single bet, say , has a 1 in chance of winning. The chance of winning is 1 out of , while the chance of losing is out of This calculator will convert "odds of winning" an event into a probability percentage chance of success. For example, you win a game if you pull an ace out of a full deck of 52 cards.

Pulling any other card you lose. How to figure odds Implied odds or betting odds are likely not the same as the true odds. Betting odds is a payout ratio that has the house profit margin built into it. Take for example the game of roulette at a casino. Popular Categories. Arts and Entertainment Artwork Books Movies. Relationships Dating Love Relationship Issues.

Hobbies and Crafts Crafts Drawing Games. All Categories. Log in Social login does not work in incognito and private browsers. Please log in with your username or email to continue. No account yet. Create an account. Learn why people trust wikiHow. Download Article Explore this Article parts.

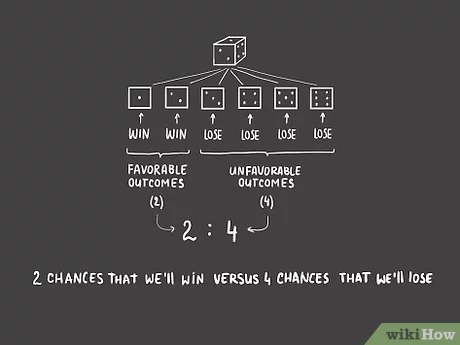
Probability Cheat Sheets. Tips and Warnings. Related Articles. Article Summary. Part 1. Determine the number of favorable outcomes in a situation. In this case, we'll just wager bets on what number the die will show after we roll it. Let's say we bet that we'll roll either a one or a two.

In this case, there's two possibilities where we win - if the dice shows a two, we win, and if the dice shows a one, we also win. Thus, there are two favorable outcomes. Determine the number of unfavorable outcomes. In a game of chance, there's always a chance that you won't win.

Count how many outcomes there are that would cause you to lose. In the example with the die, if we bet that we'll roll either a one or a two, that means we'll lose if we roll a three, four, five, or six. Since there are four ways that we can lose, that means that there are four unfavorable outcomes.

Another way to think of this is as the Number of total outcomes minus the number of favorable outcomes. When rolling a die, there are a total of six possible outcomes - one for each number on the die. In our example, then, we would subtract two the number of desired outcomes from six. Similarly, you may subtract the number of unfavorable outcomes from the total number of outcomes to find the number of favorable outcomes.

Express odds numerically. Generally, odds are expressed as the ratio of favorable outcomes to unfavorable outcomes, often using a colon. In our example, our odds of success would be 2 : 4 - two chances that we'll win versus four chances that we'll lose. Like a fraction, this can be simplified to 1 : 2 by dividing both terms by the common multiple of 2.

This ratio is written in words as "one to two odds. You may choose to represent this ratio as a fraction. In fact, we have a one-third chance of winning. Remember when expressing odds that odds are a ratio of favorable outcomes to unfavorable outcomes - not a numerical measurement of how likely we are to win. Know how to calculate odds against an event happening.

What if we want to know the odds of losing, also called the odds against us winning. To find the odds against us, simply flip the ratio of odds in favor of winning. Remember, as above, that this isn't an expression of how likely you are to lose, but rather the ratio of unfavorable outcomes to favorable outcomes.

How do you like those odds. Nfl survivor week 7 Know the difference between odds and probability. Probability is simply a representation of the chance that a given outcome will happen. This is found by dividing the number of desired outcomes over the total number of possible outcomes. It's easy to convert between probability and odds.

The answer is the number of unfavorable outcomes. Odds can then be expressed as 5 : 8 - the ratio of favorable to unfavorable outcomes. The answer is the total number of outcomes. Part 2. Differentiate between dependent and independent events. For example, if you have a jar full of twenty marbles, four of which are red and sixteen of which are green, you'll have 4 : 16 1 : 4 odds to draw a red marble at random.

Let's say you draw a green marble. If you don't put the marble back into the jar, on your next attempt, you'll have 4 : 15 odds to draw a red marble. Then, if you draw a red marble, you'll have 3 : 15 1 : 5 odds on the following attempt. Drawing a red marble is a dependent event - the odds depend on which marbles have been drawn before.

Independent events are events whose odds aren't effected by previous events. Flipping a coin and getting a heads is an independent event - you're not more likely to get a heads based on whether you got a heads or a tails last time. Determine whether all outcomes are equally likely. However, if we roll two dice and add their numbers together, though there's a chance we'll get anything from 2 to 12, not every outcome is equally likely.

There's only one way to make 2 - by rolling two 1's - and there's only one way to make 12 - by rolling two 6's. By contrast, there are many ways to make a seven. For instance, you could roll a 1 and a 6, a 2 and a 5, a 3 and a 4, and so on. In this case, the odds for each sum should reflect the fact that some outcomes are more likely than others.

Let's do an example problem. To calculate the odds of rolling two dice with a sum of four for instance, a 1 and a 3 , begin by calculating the total number of outcomes.